Mukadimah
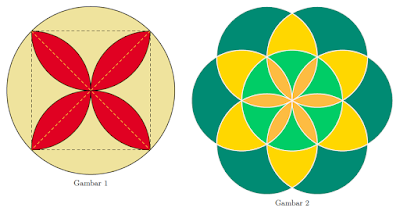
Ini tulisan kedua tentang penggunaan lingkup perintah scope dengan opsi even odd rule dan perintah clip, setelah tulisan ini. Kali ini kita akan mengambil contoh yang lebih "rumit" seperti tampak pada Gambar 2 di samping ini.Dengan menggunakan paket TikZ, kita akan menggambar tujuh lingkaran dan mewarnai bagian-bagian daerah di antaranya. Pewarnaan dibuat oleh paket xcolor dalam opsi x11names, sedangkan halaman diwarnai oleh warna paper dalam porsi 30%.
\definecolor{paper}{RGB}{239,227,157}
Lukisan
Perhatikan Gambar 1 dan Gambar 2 dalam dokumen terlampir. Kita harus membagi bidang Kartesius menjadi $6$ bagian dengan besar sudut pusat masing-masing senilai $60^\circ$. Oleh karena itu, dalam koordinat kutub, dapat kita tetapkan titik-titik $O$, $A$, $B$, $C$, $D$, $E$, dan $F$ sebagai berikut, dengan panjang jari-jari senilai $3\,\textrm{cm}$.
\coordinate (O) at (0:0);
\coordinate (A) at (0:3);
\coordinate (B) at (60:3);
\coordinate (C) at (120:3);
\coordinate (D) at (180:3);
\coordinate (E) at (240:3);
\coordinate (F) at (300:3);
Sekarang dengan berpusat pada ketujuh titik tersebut kita buat lingkaran dengan panjang jari-jari senilai $3\,\textrm{cm}$. Agar penggkodeannya lebih ringkas, kita gunakan perintah foreach sebagai berikut.\foreach \t in {O,A,B,C,D,E,F}
\draw[thick,paper!30] (\t) circle (3);
Hasilnya tampak pada Gambar 3 dalam dokumen terlampir.Berikutnya kita akan mewarnai daerah-daerah di antara ketujuh lingkaran itu. Pengkodean-pengkodean berikut ini secara berurutan diletakkan sebelum perintah foreach tadi.
Mula-mula akan kita warnai bagian daerah dari keenam lingkaran pada bagian terluar. Untuk hal itu kita akan bekerja di dalam lingkup perintah scope dengan opsi even odd rule.
\begin{scope}[even odd rule]
...
\end{scope}
Pada bagian ini kita cakup dulu daerah keenam lingkaran itu oleh\path[clip] (A) circle (3) (B) circle (3) (C) circle (3) (D) circle (3)
(E) circle (3) (F) circle (3);
Agar pewarnaan yang terjadi hanya untuk daerah dari keenam lingkaran pada bagian terluar maka kita nyatakan
\fill[PineGreen] (O) circle (3) (A) circle (3) (B) circle (3)
(C) circle (3) (D) circle (3) (E) circle (3) (F) circle (3);
Dengan demikian, pengkodean selengkapnya untuk pewarnaan dalam lingkup perintah scope itu adalah sebagai berikut.
\begin{scope}[even odd rule]
%cakupan terhadap 6 lingkaran
\path[clip] (A) circle (3) (B) circle (3) (C) circle (3) (D) circle (3)
(E) circle (3) (F) circle (3);
%mengisi warna pada bagian terluar dari daerah 6 lingkaran
\fill[PineGreen] (O) circle (3) (A) circle (3) (B) circle (3)
(C) circle (3) (D) circle (3) (E) circle (3) (F) circle (3);
\end{scope}
Hasilnya tampak pada Gambar 4 dalam dokumen terlampir.
Selanjutnya kita akan mewarnai bagian daerah lingkaran pusat/tengah dan daerah-daerah kecil yang diapit oleh dua busur dari enam lingkaran lainnya. Untuk hal itu kita kembali bekerja dalam lingkup perintah scope dengan opsi even odd rule.
Lebih dulu kita cakup lingkaran pusat itu oleh
\path[clip] (O) circle (3);
Kemudian kita isikan warnanya oleh
\fill[SpringGreen3] (O) circle (3);
diikuti oleh pengisian warna pada 6 daerah kecil yang masing-masing diapit oleh dua busur dari 6 lingkaran. Pada bagian ini (sebagai contoh) kita akan berjalan dari titik $B$ secara bersambungan untuk tiga daerah kemudian dimulai lagi dari titik $A$ secara bersambungan untuk tiga daerah lainnya.
\fill[Dandelion] (B) arc(120:240:3) %pusat A
arc(0:120:3) %pusat E
arc(-120:0:3) %pusat C
(A) arc(60:180:3) %pusat F
arc(-60:60:3) %pusat D
arc(180:300:3) ;%pusat B
Dengan demikian, pengkodean selengkapnya untuk pewarnaan dalam lingkup perintah scope yang kedua itu adalah sebagai berikut.
\begin{scope}[even odd rule]
%cakupan terhadap lingkaran pusat
\path[clip] (O) circle (3);
%mengisi warna pada lingkaran pusat
\fill[SpringGreen3] (O) circle (3);
%mengisi warna pada 6 daerah yang masing-masing diapit oleh dua busur
\fill[Dandelion] (B) arc(120:240:3) %pusat A
arc(0:120:3) %pusat E
arc(-120:0:3) %pusat C
(A) arc(60:180:3) %pusat F
arc(-60:60:3) %pusat D
arc(180:300:3) ;%pusat B
\end{scope}
Hasilnya tampak pada Gambar 5 dalam dokumen terlampir.
Terakhir, kita akan mewarnai 6 daerah yang masing-masing diapit oleh tiga busur. Pada contoh ini pewarnaan dilakukan satu persatu untuk tiap daerah itu yang masing-masing bermula dari titik $A$, $B$, $C$, $D$, $E$, dan $F$. Perintah ini diberikan secara langsung, bukan di dalam lingkup perintah scope.
\fill[Gold1] (A) arc(-60:0:3) arc(60:120:3) arc(60:0:3)
(B) arc(0:60:3) arc(120:180:3) arc(120:60:3)
(C) arc(60:120:3) arc(180:240:3) arc(180:120:3)
(D) arc(120:180:3) arc(240:300:3) arc(240:180:3)
(E) arc(180:240:3) arc(-60:0:3) arc(300:240:3)
(F) arc(240:300:3) arc(0:60:3) arc(0:-60:3);
Penutup
Sekali lagi kita cermati bahwa lingkup perintah scope beserta opsi even odd rule menentukan pewarnaan daerah secara efektif sebagaimana mestinya. Dalam hal lainnya, penetapan path tertutup untuk suatu daerah yang diapit oleh beberapa busur meminta kita untuk teliti dan cermat dalam pengacuan terhadap titik pusat lingkaran dan sudut-sudut yang bekerja untuknya.Demikian semoga bermanfaat.
$\square$ Adjie Gumarang Pujakelana 2017